|
Príklad č.8 a,b |
  
|
|
Príklad č.8 a,b |
|
a) Vypočítajte výsledný odpor sústavy medzi bodmi A,B. Po obecnom riešení vypočítajte výsledný odpor, keď poznáme : R1 = 120 Ω, R2 = 560 Ω, R3 = 270 Ω , R4 = 330 Ω ,R5 = 620 Ω, R6 = 2 kΩ.
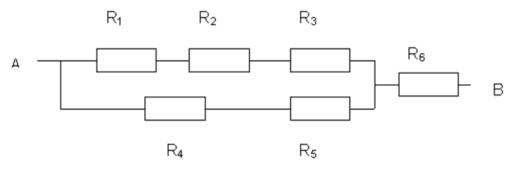
Riešenie:
Vypočítame čiastočné hodnoty odporu tých zapojení , ktoré sú jednoznačné. Celý obvod postupne zjednodušujeme, až dostaneme hodnotu výsledného odporu zapojenia !
Ra = R1 + R2 + R3 , po dosadení Ra = 120 Ω+ 560 Ω + 270 Ω = 950 Ω
Rb = R4 + R5 , po dosadení Rb = 330 Ω + 620 Ω = 950 Ω
1/Rc = 1/Ra + 1/Rb , po dosadení 1/Rc = 1/ 950 Ω + 1/950 Ω = 2/950 Ω Rc =950 Ω/2 = 475Ω
Rv = Rc + R6 , po dosadení Rv = 475 Ω + 2000 Ω = 2475 Ω
b) Vypočítajte výsledný odpor sústavy medzi bodmi A,B. Po obecnom riešení vypočítajte výsledný odpor, keď poznáme : R1 = 120 Ω, R2 = 560 Ω, R3 = 40 Ω , R4 = 330 Ω ,R5 = 620 Ω, R6 = 820 Ω, R7 =110 Ω, R8 = 180 Ω.
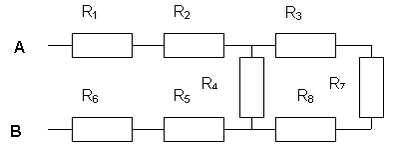
Riešenie:
Vypočítame čiastočné hodnoty odporu tých zapojení , ktoré sú jednoznačné. Celý obvod postupne zjednodušujeme, až dostaneme hodnotu výsledného odporu zapojenia !
Najprv určíme výsledný odpor sústavy R3,R7 a R8, ktoré sú zapojené v sérii:
Ra = R3 + R7 + R8 , po dosadení Ra = 40 Ω + 110 Ω + 180 Ω = 330 Ω
Tento odpor je zapojený paralelne s odporom s R4:
1/Rb = 1/Ra + 1/R4 , po dosadení 1/Rb = 1/330 Ω + 1/330 Ω = 2/330 Ω [ Rb = 330 Ω/2 = 165 Ω
Odpor Rb a všetky ďalšie odpory sú v sérii :
Rv = R1 + R2 + Rb + R5 + R6 = 120 Ω + 560 Ω + 165 Ω + 620 Ω + 820 Ω = 2285 Ω